Métricas de classificação e seus casos de uso
Neste blog, discutiremos as métricas de classificação comumente usadas. nós estaremos cobrindo Pontuação de precisão, Matriz de Confusão, Precisão, Lembrar, F-Score, ROC-AUC e logo aprenderá uma vez que estendê-los para o classificação multiclasse. Também discutiremos em quais cenários, qual métrica será mais adequada para usar.
Primeiro vamos entender alguns termos importantes usados ao longo do blog-
Verdadeiro Positivo (TP): Quando você prevê que uma reparo pertence a uma classe e ela realmente pertence a essa classe.
Verdadeiro Negativo (TN): Quando você prevê que uma reparo não pertence a uma classe e na verdade não pertence a essa classe.
Falso Positivo (FP): Quando você prevê que uma reparo pertence a uma classe e na verdade não pertence a essa classe.
Falso Negativo (FN): Quando você prevê que uma reparo não pertence a uma classe e na verdade pertence a essa classe.
Todas as métricas de classificação funcionam nesses quatro termos. Vamos inaugurar a entender as métricas de classificação
Pontuação de precisão-
Precisão de classificação é o que geralmente queremos expor, quando usamos o termo precisão. É a razão entre o número de previsões corretas e o número totalidade de amostras de ingressão.
Para classificação binária, podemos calcular a precisão em termos de positivos e negativos usando a fórmula aquém:
Accuracy=(TP+TN)/(TP+TN+FP+FN)
Funciona muito unicamente se houver um número igual de amostras pertencentes a cada classe. Por exemplo, considere que há 98% de amostras da classe A e 2% de amostras da classe B em nosso conjunto de treinamento. Portanto nosso protótipo pode facilmente obter 98% de precisão de treinamento simplesmente prevendo cada exemplar de treinamento pertencente à classe A. Quando o mesmo protótipo é testado em um conjunto de teste com 60% de amostras da classe A e 40% de amostras da classe B, logo o a precisão do teste cairia para 60%. A precisão da classificação é ótima, mas nos dá a falsa sensação de conseguir subida precisão.
Portanto, você deve usar a pontuação de precisão unicamente para dados com balanceamento de classe.
Você pode usá-lo por-
from sklearn.metrics import accuracy_score
No sklearn, há também Balanced_accuracy_score que funciona para dados de classe desequilibrados. O balanced_accuracy_score função calcula o precisão equilibrada, o que evita estimativas de desempenho exageradas em conjuntos de dados desequilibrados. É a macromédia das pontuações de recordação por classe ou, equivalentemente, a precisão bruta em que cada exemplar é ponderada de convénio com a prevalência inversa de sua verdadeira classe. Assim, para conjuntos de dados balanceados, a pontuação é igual à precisão.

Matriz de confusão-
Uma matriz de confusão é uma tábua frequentemente usada para descrever o desempenho de um protótipo de classificação em um conjunto de dados de teste para os quais os valores verdadeiros são conhecidos.

É extremamente útil para medir Recall, Precisão, Especificidade, Exatidão e, mais importante, Curva AUC-ROC.
from sklearn.metrics import confusion_matrix
Precisão-
É a razão entre os verdadeiros positivos e todos os positivos. Ele informa que, de todas as classes positivas que previmos, quantas são realmente positivas.

from sklearn.metrics import precision_score
Recall (taxa de verdadeiro positivo)-
Ele diz a você que, de todas as classes positivas, quantas previmos corretamente.
O recall deve ser o mais cimeira provável. Observe que também é chamado de sensibilidade.

from sklearn.metrics import recall_score
F1-Pontuação-
É difícil confrontar dois modelos com baixa precisão e cimeira recall ou vice-versa. Se você tentar aumentar a precisão, isso pode diminuir o recall e vice-versa. Portanto acaba em muita confusão.
Portanto, para torná-los comparáveis, usamos o F1-Score . A pontuação F1 ajuda a medir o Recall e a Precisão ao mesmo tempo.

Ele usa a Média Harmônica no lugar da Média Aritmética, punindo mais os valores extremos.
from sklearn.metrics import f1_score
Nós o usamos quando temos dados de classe desbalanceados. Na maioria dos problemas de classificação da vida real, existe uma distribuição de classe desequilibrada e, portanto, o F1-score é uma métrica melhor para julgar nosso protótipo do que a precisão.
Mas é menos interpretável. A precisão e o recall são mais interpretáveis do que o escore f1, pois a precisão mede o erro tipo 1 e o recall mede o erro tipo 2. No entanto, o F1-score mede o trade-off entre esses dois. Portanto, ao invés de trabalhar com ambos e nos confundir, usamos f1-score.
Especificidade (taxa de verdadeiro negativo): Ele informa qual fração de todas as amostras negativas foi prevista corretamente uma vez que negativa pelo classificador. Para calcular a especificidade, use a fórmula a seguir.

Taxa de Falso Positivo : FPR nos diz qual proporção da classe negativa foi classificada incorretamente pelo classificador.

Taxa de Falso Negativo: Taxa de Falso Negativo (FNR) nos diz qual proporção da classe positiva foi classificada incorretamente pelo classificador.

Veja, se você sabe claramente qual tarefa você tem que realizar, logo é melhor usar precisão e revocação ao invés de f1-score. Por exemplo, suponha que o governo lançou um esquema para detecção gratuita de cancro. Agora, é dispendioso realizar um único teste. Portanto, o governo atribuiu a você a tarefa de edificar um protótipo de estágio de máquina para identificar se uma pessoa está com cancro. Será um teste de triagem inicial, pois o governo fará previsões de seu protótipo e testará as pessoas que seu protótipo previu ter cancro, com máquinas reais para saber se elas realmente estão tendo cancro ou não. Isso reduzirá muito o dispêndio do esquema.
Portanto, nesse caso, será mais importante identificar todas as pessoas com cancro, porque podemos tolerar que uma pessoa sem cancro seja detectada uma vez que tendo cancro, porque depois de testar com máquinas reais, a verdade prevalecerá, mas não podemos tolerar um pessoa com cancro não foi detectado cancro porque isso pode custar a vida de uma pessoa. Portanto, cá você usará a métrica de recall para verificar o desempenho do seu protótipo.
Mas, se você estiver trabalhando em uma tarefa em que a precisão e o recall são também importantes, você pode usar o escore f1 em vez da precisão e do recall.
Curva ROC-AUC-
Não unicamente métricas numéricas, também temos métricas de plotagem uma vez que a curva ROC (Receiver Characteristic Operator) e AUC (Area Under the Curve).
AUC — A curva ROC é uma medida de desempenho para os problemas de classificação em várias configurações de limite. Nascente gráfico é plotado entre as taxas de verdadeiro positivo e falso positivo. A espaço sob a curva (AUC) é o resumo dessa curva que informa o quão bom é um protótipo quando falamos de sua capacidade de generalização.
Se qualquer protótipo conquistar mais AUC do que outros modelos, ele será considerado um bom protótipo entre todos os outros. Assim, podemos concluir que quanto mais AUC melhor será o protótipo na classificação de real positivo e real negativo.
- Se o valor de AUC vier uma vez que 1, podemos ter certeza de que o protótipo é perfeito ao qualificar a classe positiva uma vez que positiva e a classe negativa uma vez que negativa.
- Se o valor de AUC vier uma vez que 0, logo o protótipo é pior ao qualificar o mesmo. O protótipo irá prever a classe positiva uma vez que negativa e a classe negativa uma vez que positiva.
- Se o valor for 0,5, o protótipo terá dificuldade para diferenciar entre classes positivas e negativas. As previsões serão meramente aleatórias.
- O pausa desejado para o valor de AUC é 0,5-1,0, pois haverá mais chances de nosso protótipo ser capaz de diferenciar valores de classe positivos dos valores de classe negativos.
Vamos pegar um protótipo preditivo, por exemplo. Digamos, estamos construindo um protótipo de retorno logística para detectar se uma pessoa está com cancro ou não. Suponha que nosso protótipo retorne um pontuação de previsão de 0,8 para um paciente em pessoal, isso significa que o paciente tem maior verosimilhança de ter cancro. Para outro paciente, ele retorna pontuação de previsão de 0,2 isso significa que o paciente provavelmente não tem cancro. Mas, o que expor de um paciente com pontuação de previsão de 0,6?
Neste cenário, devemos definir um limite de classificação. Por padrão, o protótipo de retorno logística assume o limite de classificação para ser 0,5, ou seja, todos os pacientes que obtêm uma pontuação de previsão de 0,5 ou superior estão tendo cancro, caso contrário, não. Mas observe que os limites são completamente dependentes do problema. Para conseguir a saída desejada, podemos ajustar o limite. Mas agora a questão é uma vez que sintonizamos o limite?
Para diferentes valores de limite, obteremos TPR e FPR diferentes. Assim, para visualizar qual limiar é mais adequado para o classificador, traçamos a curva ROC. Uma curva ROC típica se parece com:
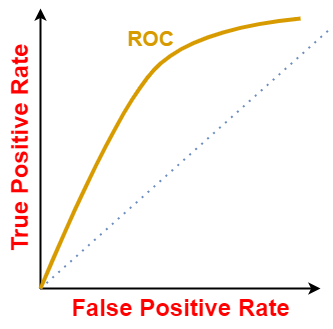
A curva ROC de um classificador aleatório com o nível de desempenho aleatório (uma vez que mostrado aquém) sempre mostra uma risca reta. Essa curva ROC do classificador aleatório é considerada a risca de base para medir o desempenho de um classificador. Duas áreas separadas por esta curva ROC indicam uma estimativa do nível de desempenho — bom ou ruim.
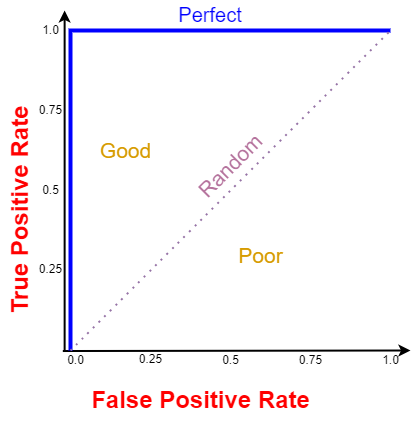
Todas as curvas ROC que se enquadram na espaço no esquina subordinado recta indicam níveis de desempenho ruins e não são desejados, enquanto as curvas ROC que se enquadram na espaço no esquina superior esquerdo indicam um bom nível de desempenho e são as desejadas. A curva ROC perfeita é indicada pela risca azul.
Valores menores no eixo x do gráfico indicam falsos positivos mais baixos e verdadeiros negativos mais altos. Valores maiores no eixo y do gráfico indicam verdadeiros positivos mais altos e falsos negativos mais baixos.
Embora a fita teórica da pontuação da curva AUC ROC esteja entre 0 e 1, as pontuações reais de classificadores significativos são maiores que 0,5, que é a pontuação da curva AUC ROC de um classificador aleatório. A curva ROC mostra o trade-off entre Lembrar (ou TPR) e especificidade (1 — FPR).
from sklearn.metrics import roc_curve, auc
Às vezes, substituímos o eixo y por precisão e eixo x por rechamada. Portanto o enredo é chamado uma vez que curva de rechamada de precisão que faz a mesma coisa (calcula o valor de precisão e rechamada em diferentes limites). Mas é restrito unicamente à classificação binária no sklearn.
from sklearn.metrics import precision_recall_curve
Estendendo o supra para classificação multiclasse
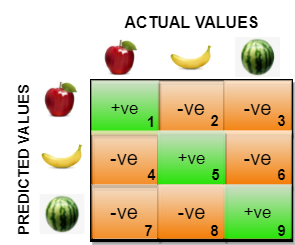
Portanto, na matriz de confusão para classificação multiclasse, não usamos TP,FP,FN e TN. Somente usamos classes previstas no eixo y e classes reais no eixo x. Na figura supra, célula1 denota quantas classes eram apple e realmente previu apple e célula2 denota quantas classes eram banana, mas preditas uma vez que maçã. Do mesmo jeito célula8 denota quantas classes eram banana, mas foram previstas uma vez que melancia.
O verdadeiro positivo, verdadeiro negativo, falso positivo e falso negativo para cada classe seria calculado adicionando os valores das células da seguinte forma:

Pontuações de precisão e rechamada e pontuações F-1 também podem ser definidas na feição multiclasse. Cá, as métricas podem ser “calculadas” em todas as classes de várias maneiras possíveis. Alguns deles são:
- micro: calcule as métricas globalmente contando o número totalidade de vezes que cada classe foi prevista corretamente e incorretamente.
- macro: calcule métricas para cada “classe” independentemente e encontre sua média não ponderada. Isso não leva em consideração o desequilíbrio do rótulo.
- Nenhum: retorna a pontuação de precisão para cada classe correspondente a cada classe.
As curvas ROC são normalmente usadas na classificação binária para estudar a saída de um classificador. Para estendê-los, você deve transmutar seu problema em binário usando OneVsAll abordagem, logo você terá n_class número de curvas ROC.
No sklearn, há também um relatório de classificação que fornece um resumo da precisão, rechamada e pontuação f1 para cada classe. Ele também fornece um suporte de parâmetro que unicamente informa a ocorrência dessa classe no conjunto de dados.
from sklearn.metrics import classification_report